This is a guest blog entry by Fotios Petropoulos.
A few months ago, Bergmeir, Hyndman and Benitez made available a very interesting working paper titled “Bagging exponential smoothing methods using STL decomposition and Box-Cox transformation”. In short, they successfully employed the bootstrap aggregation technique for improving the performance of exponential smoothing. The bootstrap technique is applied on the remainder of the series which is extracted via STL decomposition on the Box-Cox transformed data so that the variance is stabilised. After generating many different instances of the remainder, they reconstruct the series by its structural components, ending with an ensemble size of 30 series (the original plus 29 bootstraps). Using ETS (selecting the most appropriate method from the exponential smoothing family using information criteria) they produce multiple sets of forecasts, for each one of these series. The final point forecasts are produced by calculating the arithmetic mean.
The performance of their approach (BaggedETS) is measured using the M3-Competition data. In fact, the new approach succeeds in improving the forecasts of ETS in every data frequency, while a variation of this approach produced the best results for the monthly subset, even outperforming the Theta method. I should admit that the very last bit intrigued me even more to search in depth how this new approach works and if it is possible to improve it even more. To this end, I tried to explore the following:
- Is the new approach robust? In essence, the presented results are based on a single run. However, given the way bootstrapping works, each run may give different results. Also, what is the impact of the ensemble size (number of bootstrapped series essentially) on the forecasting performance? A recent study by the owner of this blog suggests that higher sample sizes result in more robust performance in the case of neural networks. Is this also true for the ETS bootstraps?
- How about using different combination operators? The arithmetic mean is only one possibility. How about using the median or the mode (both have shown increased performance in the aforementioned study by Nikos – a demonstration of the performance of the different operators can be found here).
- Will the new approach work with different forecasting methods? How about replacing the ETS with ARIMA? Or even Theta method?
To address my thoughts, I set up a simulation, using the monthly series from the M3-Competition. For each time series, I expanded the number of bootstrapped series to 300. Then, for every ensemble with sizes from 5 up to 150 members with step 5, I randomly selected the required number of bootstrapped series as to create 20 groups. The point forecasts for each group were calculated not only by the arithmetic mean but also by the median. For each operator and for each ensemble size considered, a five-number summary (minimum, Q1, median, Q3 and maximum sMAPE) for the 20 groups is graphically provided in the following figure.
So, given that the ensemble size is at least of size 20, we can safely argue that the performance of the new approach is 75% of the times better than that of Theta method (and by far always better than that of ETS). Having said that, the higher the number of bootstraps, the better and more robust the performance of the new approach is. This is especially evident for the median operator. Another significant result is that the median operator performs better at all times compared to the mean operator. Both results are in line with the conclusions of the aforementioned paper.
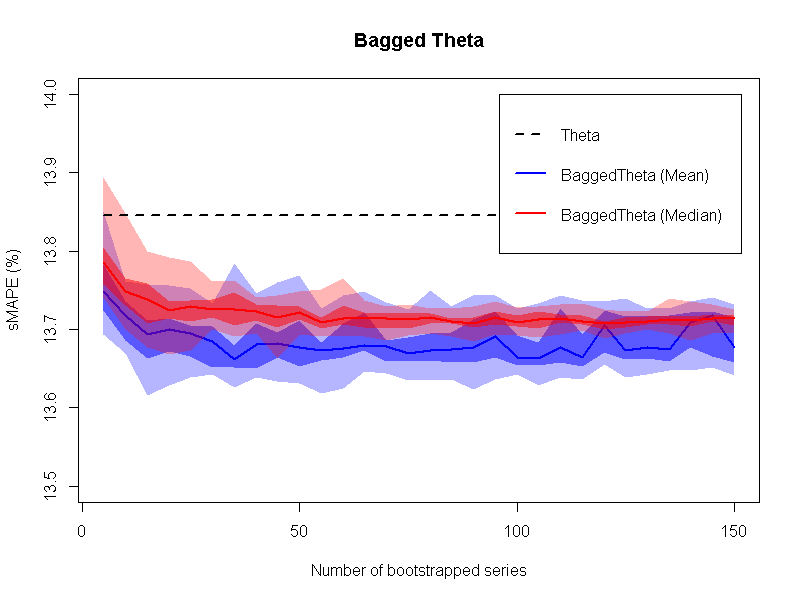
In addition, I repeated the procedure using the Theta method as the estimator. The results are presented in the next figure.
Once more, the new approach is proved to be better than the estimator applied only on the original data. So, it might be of value to check whether this particular way of creating bootstrapped time series is something that can be generalised, so that the new approach can be regarded as a “self-improving mechanism”. However, it is worth mentioning that in this case the arithmetic mean operator generally performs better than that of the median operator (at least with regards to the median forecast error), resulting, though, in more variable (less robust) performance.
By comparing the two figures, it is interesting that BaggedETS is slightly better than BaggedTheta for the ensemble sizes greater than 50. But this comes with a computational cost: BaggedETS is (more or less) 40 times slower in producing forecasts compared to BaggedTheta. This may render the application of BaggedETS problematic even for a few thousands SKUs if these are to be forecasted daily.
To conclude, I find that the new approach (BaggedETS) is a very interesting technique that results in improved forecasting performance. The appropriate selection of the ensemble size and the operator can lead to robust forecasting performance. Also, one may be able to use this approach with other forecasting methods as well, as to create the BaggedTheta, BaggedSES, BaggedDamped, BaggedARIMA…
Fotios Petropoulos (October 31, 2014)
Acknowledgments
I would like to thank Christoph Bergmeir for providing clarifications on the algorithm that rendered the replication possible. Also, I am grateful to Nikos for hosting this post in his forecasting blog.
Update 13/11/2014: Minor edits/clarifications by Fotis.