A new package for analysing and forecasting intermittent demand time series and slow moving items has been release for R. You can download the latest version from CRAN.
The launch version contains the following functions:
- crost: Croston’s method and variants.
- crost.ma: Moving average with Croston’s method decomposition.
- idclass: Time series categorisation for intermittent demand.
- simID: Simulator for intermittent demand series.
- tsb: TSB (Teunter-Syntetos-Babai) method.
Two demo time series are included to try the various functions: data and data2.
To fit Croston’s to a time series, simply use the following command:
> crost(data)
The function comes with a few different options. By default it optimises model parameters and initial values using the MAR cost function. Using the flag cost different cost functions are available. By default the smoothing parameter for the non-zero demand and demand intervals are optimised separately, but this can be controlled using the flag nop. Similarly the initialisation values for demand and intervals can be optimised or not and set either manually, or to preset initialisation heuristics. These are controlled by the flags init.opt and init.
Three different variants of the method are implemented:
- ‘croston’, for the original method.
- ‘sba’, for the Syntetos-Boylan approximation.
- ‘sbj’, for the Shale-Boylan-Johnston correction.
For example, to get SBA forecasts with optimal parameters for 12 months ahead and plot the results you can use:
> crost(data,type='sba',h=12,outplot=TRUE)
This will provide the following visual output:

Functions tsb and crost.ma allow similar level of control.
The next interesting function in the package allows you to create simulated intermittent demand series. The simulator assumes that non-zero demand arrivals follow a bernoulli distribution and the non-zero demands a negative binomial distribution. For example to create 100 simulated time series, 60 observations each, use:
> dataset <- simID(100,60,idi=1.15,cv2=0.3)
The two last inputs control the average demand interval and the squared coefficient of variation of the non-zero demand for the series.
To get a better view of the generated series, or a real dataset, we can use the idclass function. This categorises the intermittent demand time series according to existing classification schemes. In particular the following are implemented:
- ‘SBC’, classification proposed by Syntetos-Boylan-Croston.
- ‘KH’, the revised classification by Kostenko-Hyndman using the exact separation.
- ‘KHa’, as above but using the approximate separation.
- ‘PK’, the further revised classification that deals with temporal aggregation by Petropoulos-Kourentzes.
- ‘PKa’, as above but using the approximate separation.
Both ‘KH’ and ‘PK’ require the demand interval smoothing parameter of SBA as input. This can either by calculated automatically by the function, or given as an input using the a.in flag.
Finally there are two views for each classification. One summarised that merely provides the number of time series the class/method or a detailed one that provides a scatterplot of the time series characteristics. Here are some examples:
> idclass(t(dataset))
This gives by default the PKa classification.

> idclass(t(dataset),type='SBC')
> idclass(t(dataset),type='KHa')
> idclass(t(dataset),type='PK',outplot='detail')
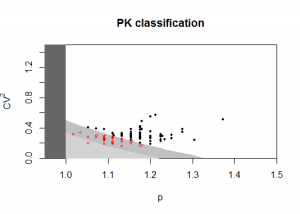
Note that the PK and KH exact classifications, unless the smoothing parameters are provided, can be computationally expensive.
More information about the various optimisation cost functions for these intermittent demand methods and the classification schemes can be found here and here. An interactive demo of various functions and optimisation options can be found here.

Dear Nikolaos,
may I ask, the interpretation from the output of function crost? I read that for intermittent data, Croston and Syntetos-Boylan is the method best used. But, the output from croston method does not seem to generate interdemand period, and somehow, the value forecasted felt underforecast.
Also, is it possible to see the plot combined with out-of-sample data and measure the forecasting methods performance with that data?
Croston’s method and its variants are separating an intermittent demand series into two components, one for the non-zero demand and one for the inter-demand interval. These two are smoothed separately, using exponential smoothing and their forecasted value is then divided to provide a `demand rate` forecast. So let’s assume that the forecasted non-zero demand is 4 and the forecasted inter-demand interval is 8. The croston forecast will be 4/8 = 0.5. Therefore, instead of producing a demand and interval forecast, you get a demand rate that combines these two. The way I read this forecast is that there will be a need for 0.5 extra units each period. Eventually over the 8 periods of the forecasted interval a total of 4 units will be in demand. The true timing of the demand event within the predicted interval is unknown and hard to predict, therefore with this method we distribute the demand over the expected interval periods, hoping that when this is translated into an inventory decision enough stock will be at hand.
To make a long story short, the forecast of Croston’s method and its variants is a demand rate forecast and not a demand forecast. This is the reason why typically we do not consider the interval forecast on its own. What you get from the crost function is the demand rate forecast. This also brings me to the second part of your comment. Measuring forecasting accuracy for Croston’s and its variants is not straightforward, as the number we get as a forecast is not a demand and therefore taking the difference between the actual demand and a croston forecast is not meaningful. I do a much better job at explaining this in this paper if you are interested.
Hi Nikolaos,
Can you please clarify or confirm if my understanding is correct?
I take data for 2 years for forecasting and the demands are intermittent. i am trying to predict for next 6 months.
Lets say i get a demand forecast of 4 units for each month for a period of 6 months.
So instead of interpreting the result as 24 units over the period of 6 months, i should interpret it as total of 4 units over the period of 6 months will be required. or 4/6=0.67 units each month?
Hi Anurag,
If I understand your description correctly you should not divide it, if your per month forecast is 4 units.
Let’s say you forecast a time series with Croston’s method and you get a per month forecast of 0.67. That would be the expected rate of demand per month (assuming monthly intermittent data). So you will observe a full unit of demand within 2 months (0.67*2), but with unknown timing. Within 6 months (lets assume that is your horizon), assuming this is your planning horizon, you would have a demand of 4 units, but of unknown timing again. These units could be in the very first month, or the last one or any in-between. Also Croston’s method is unable to actually tell you whether this demand will be clumped or not, so you may have any demand over that period that sums up to 4, but could happen in just one month, or distributed within the 6 months.
Hey Nikolaos,
Thank you for the prompt.
I get this now. But how do i measure the accuracy. I went through your paper and only able to understand that MAE and MAPE are not good measures to calculate the accuracy of the model. Any help on this please.
Many thanks.
Hi Anurag,
I realised that my reply for some reason got lost, so let me repost it. I personally prefer to use the impact on the decision variable to evaluate intermittent demand methods, therefore I prefer to directly measure the impact on inventory in my context. Nonetheless such an approach is very cumbersome to implement and computationally expensive. P. Wallström and A. Segerstedt (2010) have suggested using cumulative errors, such as the PIS which I refer to in my paper. Cumulative errors have the advantage that they overcome the “demand rate problem” of Croston’s and its derivatives, i.e. that the time series is measuring demand, while the forecast is a demand rate, as I discuss in my paper. Another interesting approach was used by R. D. Snyder et al. (2012) who used metrics that look at the prediction distributions. In my opinion this still an open question.
Hi Nikolaos,
I have intermittent demand for all my timeseries which is 36 months of history data say for 100 spares. I have used something like this for a few:
crost(abc,h=12,type=c(“sba”),cost=c(“msr”),outplot=c(TRUE))
My horizon is 12 months. Now , $frc.out is 377.4191. According to your explanation above, since crost gives the demand rate, so we can say in next 12 months we will have 377 units of demand, but cannot comment on the monthly demand rate or periods of no demand. Is there a way to generate a monthly number as well. Your help will be highly appreciated.
Thanks
Priya
Hi Priya,
The output of $frc.out should be 12 values (as you have h=12). Each of these values refers to the demand rate for each month, starting from t+1 up to t+12.
If you would calculate the sum of $frc that would the expected total demand over the complete 12 months.
Thank you for your prompt reply….really helpful
Hi Nikolaos,
I have intermittent demand for all my timeseries which is 36 months of history data say for 100 spares. I tried to use
Simulator of Intermittent Demand Series and used
dataset<-simID(n=1, obs=12, idi=1, cv2=1.085765157, level=NULL).
I calculated cv2 for one series by removing the zeroes, but i am not sure how to calculate idi or Average intermittent demand interval of each series.
If you can guide me, will be really grateful.
Priya
Hi Priya,
The command you are running constructs 1 time series with 12 observations, but no intermittency. The average intermittent demand interval (idi) is set to 1 in your example, so the time series will have demand at every interval! You would need idi > 1 to have any intermittency. For the details of either cv2 or idi you could have a look at the paper by Syntetos et al. (2005). Briefly, to calculate this you first need to find the number of observations between all non-zero demand occurrences. Then you calculate the average over these. Say you have this time series: 1, 0, 0, 4, 0, 1, 2. Then the demand intervals are 3, 2, 1 and the average interval is simply their average.
When you plot the output of the simID function in any ts.plot (time series plot) the results are reversed. So if I call testSet <- simID(n=5,obs=10,id=1.75,cv2=0.3) and I ts.plot(testSet), the x axis has 5 data points (observations) and there are 10 lines (time series). Isn't this the opposite of what we should see, as I am calling 5 time series with 10 observations?
Hi Matt,
You are correct, the command should be ts.plot(t(testSet)). This will be corrected in a latter version. Other functions in the package (e.g. idclass) assume each column to be a series, rather than row.
Thanks,
Nikos
Dear Niko,
I have a similar problem. When looking at the decomp I find an additional 1 (interval) at the beginning.
This seems to be standard in the tsintermittent.
Can you help ?
thanks
Michael
Hi Michael,
If I run crost.decomp(ts.data1) and I look at the length of the resulting intervals and demand they are the same length.
lapply(crost.decomp(ts.data2),length) gives me 8 for both. Don’t forget that there is an issue with the initialisation of the decomposition as the first interval is always unknown.
Nikos
Dear Professor,
I have one 5 year data Jan 2011 to Jan 2015, how can i forecast for Jan 2016? less available data points in R
THANK YOU
sorry, Only 5 data points from Jan 2011 to Jan2015, i want to forecast Jan2016? Could you suggest me in R with code and method?
thank you
Hi Kannappan,
I would suggest you use the
imapafunction from the tsintermittent package. To my understanding this hould be on of the safest methods to use, unless you start tweaking the settings. However, if you want to control the parameters/initial valuescrostgives you more control.Hope this helps!
Nikos
I have a time series data. How do i calculate my adi and cov2 ? Is there a package in R for the same or do i have to do it manually?
The
idclassfunction works for individual series as well. Alternatively you can usecrost.decompto get the demand size and interval series from your time series and calculate the coefficient of variation and mean interval manually.Dear Mr. Nikos
Thanks for sharing information Sir.
I called ts.data2. the data are shown :
Jan Feb Mar Apr May Jun Jul Aug Sep Oct Nov Dec
1980 0 2 0 1 0 11 0 0 0 0 2 0
1981 6 3 0 0 0 0 0 7 0 0 0 0
After that i use crost.decomp(ts.data2). The result :
$demand
[1] 2 1 11 2 6 3 7
$interval
[1] 2 2 2 5 2 1 6
I rewrite ts.data2 then insert data to new variable (testdata) as follow
testdata2<-c(0,2,0,1,0,11,0,0,0,0,2,0,6,3,0,0,0,0,0,7,0,0,0,0)
After that, I use idclass(testdata2) to know CV2 and ADI . The results show for
$cv2
[1] 0.6197917
$p
[1] 2.857143
The question is how to calculate CV2 and ADI manually? what is the formula to calculate them?
Thank you
Hi Hans,
Try this:
x <- crost.decomp(testdata2)cv2 <- (sd(x$demand)/mean(x$demand))^2p <- mean(x$interval)You can find more details in this paper.
Hi Nikolaos,
I’m using tsintermittent to produce forecasts to compare to the current state (black box) forecasts at my company. We think that our forecasts for intermittent demand are based on Croston’s. The forecasts for these products are provided as two numbers (the non-zero demand size and the interval between them). I found your paper on this very helpful, and I plan to use MAR and/or MSR to compare forecasts. However, it would be very helpful to see both parts of the forecast rather than the demand rate, since this is what our management is used to. Is there a way to output the two optimized forecasts or perhaps to reverse engineer them from the output?
Thank you
Bailey
Hi Bailey,
Let me add these two outputs to the code. It should not be too complicated. However, unless you set the smoothing parameters to something like the naive (alpha = 1) then the initialisation of the method may make the comparison problematic. I will let you know when this is updated on CRAN.
I would be interested to know which company if you can share this information (here or by email).
Thanks,
Nikos
Hi Nikos,
Thank you so much for that! I am kind of curious what you mean by the comparison being problematic though.
Bailey
Hi Bailey,
The updated package is now available on CRAN. Croston now gives an additional output
componentsthat provides the non-zero demand and intervals for the in-sample and out-of-sample periods, as well as the calculated coefficient used for SBA or SBJ corrections, if these are used. Hope this helps!Nikos
The output is linear forecast. Is there any way to convert it into intermittent demand forecast?
The output is
$components$c.out
Demand Interval
[1,] 0.992811 2.491074
[2,] 0.992811 2.491074
[3,] 0.992811 2.491074
[4,] 0.992811 2.491074
[5,] 0.992811 2.491074
[6,] 0.992811 2.491074
I am not sure what you mean by intermittent demand forecast. Croston’s method and its variants by construction will provide a linear forecast.
Can you please elaborate?
The function provides the output as non-zero demand and inter-demand interval components, but also as a final forecast
$frc.out.Nikos
Thanks Nikolaos for fast reply,
I am trying to forecast the demand which have intermittent data.
If the actual demand is intermittent, then the forecast should be intermittent right.
But croston method is giving linear forecast.
Sample Code:-
x <- rpois(20,lambda=.3)
crost(x, type='sba', h=6, outplot=TRUE)
Output:-
$frc.out
[1] 0.4210526 0.4210526 0.4210526 0.4210526 0.4210526 0.4210526
Is it possible to get the output in intermittent form. (having zeros and integers)
Thanks,
Vinod
The logic behind this method is different, so Croston’s method and its variants are unable to provide an intermittent demand as a forecast. Intermittent demand has uncertainty both in the demand size and in the demand timing and the way around trying to model this double uncertainty is instead of predicting demand per period (which should be intermittent), to predict a `demand rate’ that makes more sense as a cumulative demand over a number of periods (the lead time + review period). These methods would be unable to provide such a forecast. I am aware of a particular software that does provide a so-called `sporadic’ forecast from Croston’s method, but the calculation there is misleading. You may find useful to read this paper for more details on why the forecasts that these methods provide is useful.
Nikos
Thank You very much Nikos.
What type of format is the input data for crost()?
I don’t understand the input specification. Where should I look to find that?
Thank you,
Michael
Hi Michael,
It can be a numerical vector or a ts object. For example:
y<-c(2,0,0,1,0,3)or as a monthly time series
y.ts <- ts(y,frequency=12)I can then write either
crost(y)orcrost(y.ts)Hello Niko,
Could you please clarify the difference of the outputs $frc.out and $components$c.out ?
Thank you,
Petros
Hi Petro,
$frc.out provides the final forecasts, while the $components$c.out contains the predicted non-zero demand (first column) and the predicted inter-demand intervals (second column). If you are using standard croston then dividing these two will give you the values you get in $frc.out. If you are using any adjusted version then you will need to multiply the division result by the coefficient in $components$coeff. The $components output is aimed more for diagnostic and research purposes and for normal use the $frc.out should do the job.
Best,
Nikos
Thank you Niko,
Best wishes,
Petros
Dear Nikolaos sir,
I read the your research paper . I gone through your comments on above post. Thanks for sharing information.
I want to forecast for a intermittent part with having demand hit 5-8 in a year with very low demand size ( demand qty=1,2,3 etc.).
I use the Croston variant method to do forecact for such kind of parts but I am not satisfied with result. Can you suggest a good method from your R package- “tsintermittent”.
and if possible explain me. I am new to R programming.
example: part1- demand for (1, 0,0,0,1,1,2,0,0,0,0,1,2,0,0,0,0,0,1,1,1,1,1) like this I want o forecast for next 3 month .
Please help me
Thanks
Dnyaneshwar
Hi Dnyaneshwar,
I think one of the more robust methods to use for forecasting intermittent time series is imapa from the tsintermittent package. However an important question here is what is the criteria of a good forecast in your case? Good performance in intermittent demand context is quite hard to define and simply calculating typical error metrics, such as MSE or MAE (MAD) is misleading.
Nikos
Thank you Nikos for fast reply.
Hi Nikos,
I have a data from 1st Jan 2014 to 1st August 2017. It is an intermittent demand case.
data is something like this
2014-01-01 2014-01-01 2014-01-01 2014-01-02 2014-01-02 2014-01-03 2014-01-03 2014-01-03
0 0 0 0 0 0 0 0
2014-01-03 2014-01-04
0 0
etc. there are values in later period.
I want to forecast for next 30 days.
I ran this code:
x 0.1917784
so, is it means that for next 30 days I must have a stock of 30* 0.1917784 ???
Also, what other things i can interpret from this model???
Also, what is next step to validate this model , means procedure to calculate MASE (mean absolute scaled error)?
Thanks in advance
code is
x<-crost(g,h=30x<-crost(g,h=30)
where g is dataset
0.1917784 is x$frc.out value
Hi MG,
The 30*0.1917784 would be the expected cumulative demand over the next 30 days, but without accounting for uncertainty. Normally you need to introduce some safety stock to account for this uncertainty. This depends on the inventory policy you want to use and so on. I would recommmend you have a look at my intermittent demand papers for a discussion on this. I think the most detailed is given on this one: http://kourentzes.com/forecasting/2013/04/19/intermittent-demand-forecasts-with-neural-networks/
As for the error metric to use, well in the same paper I argue that error metrics, especially these type of error metrics are not great for validating intermittent demand forecasts, and only an inventory simulation provides a conclusive evaluation. The problem for instance of MASE is that it prefers 0 forecasts, i.e. a forecast being zero all the time would typically be preferred by the metric, even if such a forecast is useless. The reason for this is that due to the absolute in the error metric it looks for the median of your actuals and not the mean as we would normally anticipate. The median of intermittent demand time series is often 0.
Nikos
Hi Nikolaos,
I was wondering if TSB or SBA method can also help in the cases where demand sizes are not small? like they are medium sized (above 100 items per month)
Thank you!
Lissa
Hi Lissa,
If the demand becomes continuous then Croston’s method becomes the same as Single Exponential Smoothing. The same is true for TSB. SBA that adjusts Croston’s method forecasts would provide biased forecasts, so it would be inappropriate. If the demand is still intermittent, but of high volumes, then the classification scheme used to distinguish between Croston’s and SBA would tend towards SBA all the time, but we do not have a good way to choose between SBA and TSB. I do not see any particular reason that TSB is inappropriate apart from that it is looking for obsolescence.
Thank you for your reply, Nikos. I am not sure if I quite understand obsolescence. What does it mean in the intermittent demand context?
Think about an item that you expect it to go out of market. For example, spare parts for an old car that is no longer sold, or towards end of product lifecycle, but still supported by a company in terms of service. The demand for spare parts will also gradually decrease. These gradual decrease in demand, to the point that demand will be zero, is what we try to model with TSB. If this obsolescence is not modelled, then for items that are very intermittent you will end up with excess stock when the item is indeed no longer sold.
Hi!
Love the package for my intermittent demand so far. I got a question on the data.frc function with method as “auto”.
I keep running into the below error, not sure if there is any way to get around this?
Error in vector(“list”, sum(cls$summary)) : object ‘cls’ not found
There was a bug that had slipped through. I have fixed it and I will push an update to CRAN for this shortly.
Thanks!
Nikos
Hi Nikos,
I am facing the same problem, and I was wondering whether the updated version has already been made public.
Thank you for this amazing package!
Hi Sarah,
I have setup a development repository for the package: https://github.com/trnnick/tsintermittent
You can find the latest version there. In the examples I am running the functions seem to work fine. If you want, please send me a example dataset that does not work to see how I can fix it.
Thanks!
Hi Nikos,
thank you for the package, very useful for spare parts forecasting. Unfortunately, data.frc still fires “Error in vector(“list”, sum(cls$summary)) : object ‘cls’ not found”
The data:
date quantity
200601
200602
200603
200604
200605
200606
200607
200608
200609
200610
200611
200612
200701
200702
200703
200704
200705
200706
200707
200708
200709 1
200710
200711
200712
200801
200802
200803
200804
200805
200806
200807
200808
200809
200810
200811
200812
200901 1
200902
200903
200904
200905
200906
200907 1
200908
200909 2
200910
200911
200912
201001
201002
201003
201004
201005
201006
201007
201008
201009
201010 2
201011
201012
201101
201102
201103
201104
201105
201106
201107
201108
201109
201110
201111
201112
201201
201202
201203
201204
201205 4
201206
201207
201208
201209
201210
201211 10
201212
201301
201302
201303
201304
201305
201306 1
201307 4
201308
201309
201310
201311 4
201312
201401 1
201402
201403
201404
201405
201406
201407 4
201408
201409
201410
201411
201412
Hi Irene,
I cannot reproduce the error in my case. Do you want to email me some data & code?
Thanks,
Nikos
Hi Nikos,
first of all, I want to thank you for sharing this wonderful package.
I try to compare the performance of different sales forecast methods with each other. That`s why I would like to receive actual point forecasts from the croston`s method. I understand why a demand rate is more appropriate for forecasting intermittent time series, nevertheless I would like to receive point forecasts for comparison.
In an earlier post you refered to particular software, that provides ‘sporadic’ forecasts. (21th April, 2016)
Even when the calculations in this software is misleading, I would like to ask if it is possible to use this software in R?
Johannes
Hi Johannes,
Thanks! It is possible, but I advise against it. You can find the demand size and demand interval forecasts separately at the output
$components. There you will findc.outthat has a column for the demand size and one for the interval. You will also find$coeffthat would be the scaling factor for SBA. So if you want to simulate the output of SAP (which again I stress that it is wrong!) you can use the following set of commands:fit <- crost(ts.data1) horizon <- 20 forecast <- rep(0,horizon) forecast[seq(TRUE,horizon,round(fit$components$c.out[1,2]))] <- fit$components$c.out[1,1] print(forecast) Consider that if you want to produce the forecasts in this way there is no guideline if you should start from the first period or not (for instance, in the example above the forecasted demand is put at the 1st and 11th period, but could very well be at the 10th and 20th) and whether we should round up or down the interval. Hope this helps!
Nikos
I want to compute Average Demand Interval for a set of demand databse. Can you please let me know how this will work in this package?
Sample Data is as under
Date Demand
1 3
2 0
3 0
4 1
5 0
6 1
Hi Lalit,
You would need to use the crost.decomp function. This will give you two vectors: (i) demand; and (ii) interval.
All you need then is to calculate the mean of the interval.
Thanks Nikos
Hi Nikos,
i have a dataset of 1510 products having intermittent demand over 24 time periods. I am using croston methond to forecast demand. I am using the crost() method from tsintermittent package. below is my code:
z=matrix(Intermittent_Dataset_Cleaned)
mycroston <-function (x)
{
y=crost(x,h=3,init="mean",type="croston",w=NULL)
return(y)
}
for(i in 1:1510)
{
forecast[i]=mycroston(z[i])
}
The above code obviosuly won't work. Could you help me figure out a way, where I could just return the $frc.in on calling the function and store it in forecast matrix.
I am new to R, any help would be greatly appreciated.
Thanks,
Prerna
Hi Prerna,
The easiest way is to use the function
data.frc. For this to work you need to have your data as a data.frame, where each column is a time series to be modelled and each row is a time period.The the call you need is:
forecasts <- data.frc(Y,method="crost",h=3)Then a matrix with all the forecasts is available:
forecasts$frc.outWith this function you can call other forecasting methods that exist in tsintermittent as well. Have a look at the documentation.
In the function above to make it work all you need to do is change the croston line to:
y=crost(x,h=3,init="mean",type="croston",w=NULL)$frc.outHi,
Thank you for you response. i tried running my function. I keep getting the error:
Error in crost(x, h = 3, init = “mean”, type = “croston”, w = NULL) : (list) object cannot be coerced to type ‘double’.
I also tried
forecasts=data.frc(z,method=”crost”,h=3) and the error that I get is:
Error in FUN(newX[, i], …) : (list) object cannot be coerced to type ‘double’
Could you please point me to what I am doing wrong here?
Thanks again,
Prerna
Can you describe x? What is its class (use
class(x)) and its size?Hi,
I am taking a different approach now. However, I am running into a different problem:
z=data.frame(Regular0_1Cases)
forecasts0_1=data.frc(z,method=”crost”,type=”croston”,h=3)$frc.in
forecasts0_1$frc.in
forecasts0_1$frc.in is constantly showing to be null.
I do get values for $frc.out.
Could you please tell me why $frc.in is showing null?
Thanks,
Prerna
Hi Prerna,
This really depends on the in-sample data. How many observations are there, when the first non-zero demand occurs and what settings you are using.
From what I understand it seems that the in-sample is probably too short?
Nikos
There are 24 observations each series in the dataset. First non zero can be any where in the 24 periods.
Thanks,
Prerna
I cannot think of a reason that you do not get in-sample fit with the information I have. Can you be more specific?
Hi, I am new to those methods and try to implement the SBA method to spare parts demand forecasting. Is it also possible to perform the analysis in Excel?
Yes, it is possible to do this in excel, but it is not easy to automate in excel due to the decomposition required for Croston’s method. AN example of how to do this in excel can be found in this spreadsheet. This will help you produce a Croston forecast. To adjust this to become into SBA you will need to multiply the forecast by 1-(a/2), where a is the smoothing parameter for the intervals time series (the denominator in Croston’s method). Keep in mind that in excel getting optimal values for the initial values and the smoothing parameters can be quite messy.
Nikos
Hi Nikos,
Thank you very much for the spreadsheet attached. I had a look at it and it looks quite straightforward. As I see though, the method consistently underestimates the forecast compared to the actual values.
Why do you think it is messy to find optimal values for the parameters and the initial values? Initial values are known, right? And the solver should make it possible to calculate the optimal smoothing parameter I think? Maybe you can explain me where you are refering to?
I do have two questions left:
– Can I also use a weekly period instead of a monthly period?
– Is it possible to use this data in order to set optimal inventory levels given a certain service level? Or can I find a paper on how to do this?
Thank you very much in advance!
The underestimation is up to a point due to the initialisation and parameters of the method and also potentially due to the way that the forecast is assessed. This paper may be helpful, it discusses all three aspects and also explains what I meant by “messy” to find optimal values.
As to your other questions: i) yes, you could use any frequency, the method is still applicable; ii) this really depends on the inventory policy you are using. On the top of my head I cannot think of a paper that is transparent enough on this (though the aforementioned paper discusses some of these aspects). Perhaps a textbook on operations and inventory (the new edition of Silver’s book is out) would be the best starting point.
Hi Nikolaos,
Great post. I am using your package in R to generate the demand forecast. I was wondering if the package handles obsolescence of product or not? If not is there a way to extend the package?
I am referring to the following paper: https://arxiv.org/abs/1409.1609
Thanks,
Jayash
Hi Jayash,
Thank you for the paper – unfortunately I have not implemented that specific method in the package. Currently, only TSB is available to deal with obsolescence of products. My intention is to do a major update of the package structure first, before i get the time to introduce new functionalities. I hope the time to do that soon!
Best,
Nikos
Hi Nikos,
Thanks for the response, much appreciated. TSB works fine for my use-case. I look forward to the updates. 🙂
I was wondering if there is a way to generate sample paths (through simID or similar simulation function) and update the mean, idi, CV2 along the sample path. This will introduce auto-correlation in the sample paths. Or will that be a violation of the assumptions of intermittent demand.
Thanks again.
Jayash
Hi Jayash,
Currently simID does not offer this. As for the “assumptions of intermittent demand”, I am of the opinion that our intermittent demand methods are so messy and incomplete (or our data generating models) that violating standard practice assumptions is fine, given that the resulting model/method performs better on real data after being rigorously evaluated. My paper on predicting intermittent demand with neural networks follows exactly this logic, I drop the assumption of independence between demand size and intervals that is typical in Croston’s method and its variants (including TSB), as well as assumed data generation processes and demonstrate gains on real data. Of course that paper has its limitations, but I think it makes a valid point in moving beyond the standard approaches in modelling intermittent demand data.
Best,
Nikos
Hi Nikos,
Thanks for the explanation. I had read your paper and thanks for bringing it to my attention again in this context. I will try to implement a NN for my use case and see how it performs.
Thanks again,
Jayash
Hi Nikolaos,
Great package! Many thanks for sharing.
I was wondering if TSB or Croston method can support the idea of so-called ‘black holes’ inside of an input time series. In my case demand is generated from the website that simply doesn’t show a product that is out of stock for some period of time, so even there was some demand in real world it can’t be observed. I guess I am doing something incorrect setting zero demand for particular points.
Best
Valery
Hi Valery,
If I understand correctly your problem currently none of the methods in the package would do the trick. I think setting theae periods to zero is not appropriate as it would make the methods think tbat the interdemand periods are longer. So adapted method should be devised for this problem. Could you share an example perhaps? Thanks!
Hi Nikolaos,
Thanks for your prompt reply!
Yes, this issue with the fake interdemand periods is exactly what I am concerning about. The typical example is below. [Nikos: data cropped]
Interesting! I think I know how this can be dealt with, but I will need some time to code a solution. But I do not have a good view how well it will work!
Do you have several time series that could be used to test a potential solution?
Nikos
P.S. I cropped the time series from the post above to keep the comment size small!
Hi Nikolaos,
Sure, I have plenty of such data. Just uploaded a chunk of it here:
https://drive.google.com/file/d/0B_ifQOusmJeFX3FzUVdHSnV5TG8
I use 28 days forecasts and obviously try to minimize stock-outs so for the forecast accuracy evaluation I select time series that contain at least 28 days long period with avail=1. In other words, I try to predict demand in case everything is on stock.
Best
Valery
Dear Nikos,
I am currently working on a simulation optimisation of a replenishment problem with stochastic intermittent seasonal (lumpy sometimes) demand.
What I intend to do is to generate stochastic intermittent demand in excel, however I am unsure about some things:
* Should I only use the period between the first and the last demand to estimate the ADI and CV2 with the package? (leaving the period before and after this out, where the demand is 0)
* would it be appropriate to simulate a demand frequency with the ADI and standard deviation of the ADI assuming a normal distribution, e.g. IF norm.inv( rand() , ADI , st.dev. ADI) 0 then norm.inv( rand() , ADI , st.dev. ADI). And then by doing the same for the demand size?
I hope to hear from you!
Regards
Pepijn
Hi Pepijn,
The way I see it seasonal intermittent demand is an oxymoron. If it is seasonal, then the demand event timing is known (it is seasonal), so you are left with only one type of variation, the one on the demand size. In this case one could model the process with a regression with dummies. A few colleagues have supported the idea of seasonal intermittency, but I have to yet see a convincing process for it. If the seasonality is on the arrival rate, then you would need to simulate your data using a Poisson regression with a time varying (in a seasonal manner) arrival rate. So unfortunately I cannot answer your questions in a helpful way, as I do not think that simulating demand like that is helpful. Nonetheless, for your first question you do not need to edit your data, just use all. For your second question, I would suggest you check the simID function in the package. That should give you a few ideas.
Best,Nikos
Dear Nikos,
thank you for your reply!
I understand what you mean, but when I look at the data, I find that between June – september the demand has a very irregular and had weeks of no demand followed by peaks of demand or more intermittent-like lower demand, if I would be able to zoom in more (which I unfortunately can’t because I have data on a week basis) the demand (in those months where product is sold) would be even more intermittent.
Would you still argue that it would be unwise to model the demand as intermittent/lumpy for those months in which I observe demand?
Fitting distributions so far has not worked..
regards
Pepijn
this is, for example, the demand of a store during the summer months (per week), and demand in the months afterwards is 0
0
0
0
8
0
0
4
2
0
1
1
0,0
1,0
2
0,0
2
1
1
3
0
0
0
0
0
0
0
0
0
0
I see. Is this pattern similar over the years? Surely standard intermittent demand methods will be unable to deal with this case. I do not think that there is any standard method that deals with such data, so this is a case that something new should be trialed. To your question, is it unwise to model it as intermittent/lumpy demand? I do not know, but I think I would still try to take advantage of the seasonal aspect in a very explicit way, using for example a regression.
Interesting problem!
Hi Nikos,
a short question: is a function like accuracy from the forecast package planned for tsintermittent? Thank you.
Unfortunately not. Though I am in the process of redesigning the tsintermittent package to make it combatible with the logic of the forecast package (and thief, hts, MAPA, smooth, etc…). I hope in the coming weeks to have finished this and post an update!
Dear Nikolaos,
I will also echo the many folks, from the community for such a great package.
What I have been struggling with is not analyzing sparse demand but generating a similarly sparse forecast.
For example
0
0
500
0
0
450
0
0
500
0
0
450
I would like to see a forecast that isn’t ~160 every period but instead has two periods of 0 followed by ~475..
Any insights would be appreciated.
Thank you and Regards
Nadav
Hi Nadav,
The problem in producing such a forecast, in the context of interemittent demand, is that the timing of the demand event is uncertain. Intermittent demand is characterised by uncertainty both in the demand size and demand interval. If the uncertainty on the interval is minimal then it is be possible to produce such as forecast, and probably regression would be a good way to do it, where the periods of zero demand can be easily modelled. For example, in your case you could build a regression that the intercept is set to zero and you have a dummy variable to indicate the demand event, where the regression forecast would return something like: 0, 0, 475, 0, 0, 475, … Alternatively you could approach this problem as a seasonal forecasting problem, where an additive exponential smoothing would probably do the trick.
May I ask, what application produces that type of data?
Hi Nikos,
Retail orders from manufacturer often take such a pattern, although less clean than the example provided.
The retailer has a specific inventory threshold that triggers an order which is usually a given lot size.
Manufacturer’s have ready access to the order patters but little insight to inventory levels or buyer habits.
A systematized way of analyzing many such time series could help manufacturer’s plan better from a production perspective as well as warehouse stocking.
Regards
Nadav
Thanks! My response was along the lines of a specific data generating process, but this does not seem to be the case here. In this case you may find this work quite relevant. When you consider forecasting across multiple tiers of the supply chain it is quite beneficial to build models that have both views, if point-of-sale information is available.
The link is intriguing and I will have to delver into it deeper.
When I first started in supply chain in the year 2000, readily available point of sale data was coming anytime now. Looking at larger markets such as the US and Asia very little gain has been made by manufacturers. They have access to POS data for some retailers and not other and it takes considerable effort and cost to get the information.
Other areas such as Australia seem to be the exception and POS data looks to be readily available for most major retailers.
One followup question, for a model such as Croston’s is the frequency of non-zero demand and the magnitude or say amplitude of the non-zero demand readily available outputs?
Thanks
Nadav
Yes! Check the
$componentsoutput.With regards to POS, this is a good point. We found that we did not need all the POS data from different retailers to achieve the gains, and only the major retailers were enough.
Hi Nikos
Which initialization method is used, when I use the Crost() function i R ?
And how are the weights optimized ?
Hi Peter, this is paper that explains how this is done (and why!): https://kourentzes.com/forecasting/2014/06/11/on-intermittent-demand-model-optimisation-and-selection/
Hi Nikolaos,
Great package! Many thanks for sharing.
I am trying to forecast it but facing some problem.
This is for e.g. my dataset and I am trying to use the package.
Date Expenses
01-07-2006 18
01-08-2006 0
01-09-2006 0
01-10-2006 0
01-11-2006 30
01-12-2006 15
01-01-2007 0
01-02-2007 18
01-03-2007 177.78
01-04-2007 0
01-05-2007 0
01-06-2007 0
01-07-2007 30
01-08-2007 44.2
01-09-2007 0
01-10-2007 62.1
01-11-2007 0
01-12-2007 95.89
01-01-2008 0
01-02-2008 0
01-03-2008 252.7
01-04-2008 97.29
01-05-2008 327.3
01-06-2008 0
01-07-2008 0
01-08-2008 39
01-09-2008 232.19
01-10-2008 20.1
01-11-2008 0
01-12-2008 17.4
01-01-2009 0
01-02-2009 169.02
01-03-2009 0
01-04-2009 0
01-05-2009 252.7
01-06-2009 0
01-07-2009 451.07
01-08-2009 60
01-09-2009 35.01
01-10-2009 13.56
01-11-2009 0
01-12-2009 0
01-01-2010 0
01-02-2010 0
01-03-2010 0
01-04-2010 577.02
01-05-2010 0
01-06-2010 0
01-07-2010 9
01-08-2010 78.68
01-09-2010 67.5
01-10-2010 15
01-11-2010 0
01-12-2010 0
01-01-2011 0
01-02-2011 0
01-03-2011 0
01-04-2011 36.59
01-05-2011 40.5
01-06-2011 60
01-07-2011 30
01-08-2011 0
01-09-2011 37.5
01-10-2011 37.5
01-11-2011 30
01-12-2011 210
01-01-2012 127.5
01-02-2012 37.5
01-03-2012 89.23
01-04-2012 460.78
01-05-2012 903.9
01-06-2012 506.9
01-07-2012 0
01-08-2012 0
01-09-2012 0
01-10-2012 265.01
01-11-2012 0
01-12-2012 3054.4
01-01-2013 612.73
01-02-2013 1304.3
01-03-2013 0
01-04-2013 0
01-05-2013 520.5
01-06-2013 995.24
01-07-2013 716.72
01-08-2013 569.53
01-09-2013 120.25
01-10-2013 578.43
01-11-2013 52.5
01-12-2013 97.5
01-01-2014 120
01-02-2014 30
01-03-2014 0
01-04-2014 0
01-05-2014 199.17
01-06-2014 45
01-07-2014 305.51
01-08-2014 457.12
01-09-2014 0
01-10-2014 0
01-11-2014 46.14
01-12-2014 0
01-01-2015 0
01-02-2015 0
01-03-2015 15
01-04-2015 0
01-05-2015 30
01-06-2015 1588.93
01-07-2015 0
01-08-2015 17.4
01-09-2015 0
01-10-2015 0
01-11-2015 5631.07
01-12-2015 0
01-01-2016 0
01-02-2016 0
01-03-2016 37.5
01-04-2016 809.2
01-05-2016 465.39
01-06-2016 0
01-07-2016 0
01-08-2016 156.92
01-09-2016 318.01
01-10-2016 678.51
01-11-2016 0
01-12-2016 0
01-01-2017 4372.84
01-02-2017 0
01-03-2017 0
01-04-2017 507.05
01-05-2017 112.5
01-06-2017 0
01-07-2017 0
01-08-2017 37.5
01-09-2017 0
01-10-2017 0
01-11-2017 0
01-12-2017 0
01-01-2018 1135.78
01-02-2018 489.48
01-03-2018 39
01-04-2018 0
01-05-2018 0
01-06-2018 1048.76
01-07-2018 78
01-08-2018 0
01-09-2018 0
01-10-2018 0
01-11-2018 1144.04
01-12-2018 276
01-01-2019 0
01-02-2019 0
01-03-2019 1161
01-04-2019 0
01-05-2019 1759.37
01-06-2019 97.5
Thanks! It appears your question got truncated, can you please repost your question?
Hi Nikolaos,
I was trying to understand the difference between the results produced by TSB and Croston. I believe Croston returns expected demand per period whereas TSB returns a point forecast. I have 2 questions here –
1) Assuming I want the forecasts for the next 5 periods and TSB function returns 10 units as forecast. Should I infer that in each forecast period I can expect a demand of 10 units? Hence, at the end of 5 periods, I will be expecting a demand of 50 units
2) How to incorporate seasonality and trend into Croston and TSB? One way I read was to use (S)ARIMA or Holt-Winters. I was wondering if it is possible to use Holt-Winters instead of simple exponential smoothing (SES) in Croston or TSB?
1) I interpret both as having the same style of output, so the forecast for each period is the units per period, and across the lead time you need to take the sum.
2) That has been a question that has been bugging me for a while myself. I think now we have a reasonable answer to this. Have a look at some of my later work.
Hi Nikos,
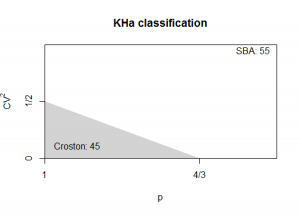
Can you give some more information about the KHa and KH categorization.
Is it based on the equation :
v > 2-3/2p, (Then SBa else Croston)
where v is coefficient of variation of non zero demand squared and p is average inter-demand interval
It is from a note by Kostenko and Hyndman (you can find the detail here), which is an exact solution of Syntetos and Boylan’s work that uses the separation margin you mention. In KH and KHa that margin is considering the smoothing parameter as well. Practically speaking the difference between the schemes is not that severe. We have extended this a bit to exclude series that have very low intermittency, but eventually I think there is a better way to handle the problem.
Hi Nikolaos! I’m a beginner in R
What I have: Sales_date.csv contains the historical daily unit sales data per product ( 3 colums: Product name, Demand, Date)
What I want to do: categorize the demand off all the products into 4 groups (lumpy, intermittent, smooth, erratic) by using two factors: (i) average demand interval (ADI) cut off value 1.32 and (ii) square coefficient of variation of demand sizes (CV2), cut off value 0.49.
Then allocate suitable forecasting method to each group (Croston or SBA method or single exponential smoothing)
I’ve tried using tsintermittent package in RStudio based on the code from https://github.com/trnnick/tsintermittent/blob/master/R/idclass.R. (fuction idclass to categorize the demand), but it did not work.
It would be highly appreciate if you could please guide me the right way to use the code in my case
Thank you very much in advance
Hi Stephanie!
You will need to arrange the data in a more time-series friendly way, where each column will be a time series. Date information is not important for this, but it will not complain if it is there. So what you want is each column to be a product, and each row to be a demand figure. Then idclass should be able to work.
Since you are a beginner in R, you may find it helpful to master the data types a bit, especially the ts() class that most forecasting algorithms use.
On another note though, I still find this classification very handy for understanding my data, but not so useful for forecasting, once you are optimising your forecasting models, so depending what you are trying to do, if this gets too fussy, you may just skip it!
Dear Prof. Nikolas,
I have a questions that bothered Me all the time. Does the intermittent data have to have a very strong autocorrelation? Thank you in advance.
Sincerely
Muhaimin
A very good question, for which I do not have a simple yes/no answer.
Can we calculate autocorrelation on intermittent data? Sure we can, but it doesn’t seem to give us the intuition we expect, as implicitly it tells us the information on an assumed ARIMA structure (that is not from the definition of autocorrelation, but from the practicalities of it!). Is an ARIMA valid for intermittent data? We typically say no, as the demand will often be characterised by non-negative low count integer values. In that sense an Integer Valued ARMA might be more fitting (INARMA; there is some work on INARMA and intermittent series). So that would suggest that our typical autocorrelation does not apply to intermittent series. On the other hand, if we consider the information contained in the time series, and temporally aggregate it (see here) at some point it will behave more like a normal time series, at which point autocorrelation will be valid and usefull. Where does this leave us? My intuition is that although we could calculate it, to me it appears it would be misleading. Is there in a looser term possibility of autocorrelation? Sure there is, and we can observe it at temporally aggregate views of the intermittent time series.
So to your question, does intermittent daya have to have a very strong autocorrelation. I don’t think there is such a requirement, and even if there was, I personally wouldn’t know what to do with it!
Thank you very much, sir. I’m working on my thesis and dealing with intermittent time-series data. Introduce me is a student at NCTU-Taiwan. Once again, thank you very much for your answers, sir. Very helpful.
Sincerely
Muhaimin